觀點 | 圖靈獎得主Judea Pearl：機器學習的理論侷限性與因果推理的七大特性

論文地址：http://ftp.cs.ucla.edu/pub/stat_ser/r475.pdf

 

當前的機器學習幾乎完全是統計學或黑箱的形式，從而爲其性能帶來了嚴重的理論侷限性。這樣的系統不能推斷干預和反思，因此不能作爲強人工智能的基礎。爲了達到人類級別的智能，學習機器需要現實模型（類似於因果推理的模型）的引導。爲了展示此類模型的關鍵性，我將總結展示 7 種當前機器學習系統無法完成的任務，並使用因果推理的工具完成它們。

 

 

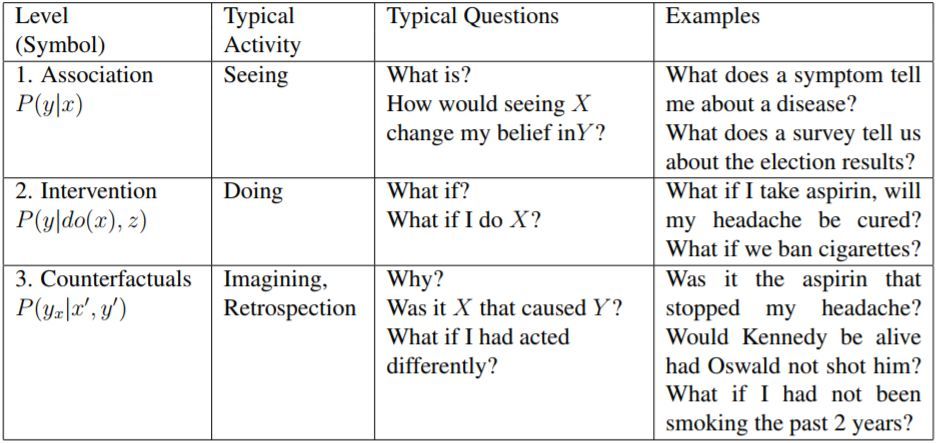
圖 1：因果關係的類型

 

因果推理模型的 7 種特性

 

考慮以下 5 個問題：

 

• 給定的療法在治療某種疾病上的有效性？

   

• 是新的稅收優惠導致了銷量上升嗎？

   

• 每年的醫療費用上升是由於肥胖症人數的增多嗎？

   

• 招聘記錄可以證明僱主的性別歧視罪嗎？

   

• 我應該放棄我的工作嗎？

   

這些問題的一般特徵是它們關心的都是原因和效應的關係，可以通過諸如「治療」、「導致」、「由於」、「證明」和「我應該」等詞識別出這類關係。這些詞在日常語言中很常見，並且我們的社會一直都需要這些問題的答案。然而，直到最近也沒有足夠好的科學方法對這些問題進行表達，更不用說回答這些問題了。和幾何學、機械學、光學或概率論的規律不同，原因和效應的規律曾被認爲不適合應用數學方法進行分析。

 

這種誤解有多嚴重呢？實際上僅幾十年前科學家還不能爲明顯的事實「mud does not cause rain」寫下一個數學方程。即使是今天，也只有頂尖的科學社區能寫出這樣的方程並形式地區分「mud causes rain」和「rain causes mud」。

 

過去三十年事情已發生巨大變化。一種強大而透明的數學語言已被開發用於處理因果關係，伴隨着一套把因果分析轉化爲數學博弈的工具。這些工具允許我們表達因果問題，用圖和代數形式正式編纂我們現有的知識，然後利用我們的數據來估計答案。進而，這警告我們當現有知識或可獲得的數據不足以回答我們的問題時，暗示額外的知識或數據源以使問題變的可回答。

 

我把這種轉化稱爲「因果革命」（Pearl and Mackenzie, 2018, forthcoming），而導致因果革命的數理框架我稱之爲「結構性因果模型」（SCM）。

 

SCM 由三部分構成：

 

1. 圖模型

    

2. 結構化方程

    

3. 反事實和介入式邏輯

    

圖模型作爲表徵知識的語言，反事實邏輯幫助表達問題，結構化方程以清晰的語義將前兩者關聯起來。

 

接下來介紹 SCM 框架的 7 項最重要的特性，並討論每項特性對自動化推理做出的獨特貢獻。

 

1. 編碼因果假設—透明性和可試性

 

圖模型可以用緊湊的格式編碼因果假設，同時保留透明性和可試性。其透明性使我們可以瞭解編碼的假設是否可信（科學意義上），以及是否有必要添加其它假設。可試性使我們（作爲人類或機器）決定編碼的假設是否與可用的數據相容，如果不相容，分辨出需要修改的假設。利用 d-分離（d-separate）的圖形標準有助於以上過程的執行，d-分離構成了原因和概率之間的關聯。通過 d-分離可以知道，對模型中任意給定的路徑模式，哪些依賴關係的模式纔是數據中應該存在的（Pearl，1988）。

 

2. do-calculus 和混雜控制

 

混雜是從數據中提取因果推理的主要障礙，通過利用一種稱爲「back-door」的圖形標準可以完全地「解混雜」。特別地，爲混雜控制選擇一個合適的協變量集合的任務已被簡化爲一種簡單的「roadblocks」問題，並可用簡單的算法求解。（Pearl，1993）

 

爲了應對「back-door」標準不適用的情況，人們開發了一種符號引擎，稱爲 do-calculus，只要條件適宜，它可以預測策略干預的效應。每當預測不能由具體的假設確定的時候，會以失敗退出（Pearl, 1995; Tian and Pearl, 2002; Shpitser and Pearl, 2008）。

 

3. 反事實算法

 

反事實分析處理的是特定個體的行爲，以確定清晰的特徵集合。例如，假定 Joe 的薪水爲 Y=y，他上過 X=x 年的大學，那麼 Joe 接受多一年教育的話，他的薪水將會是多少？

 

在圖形表示中使用反事實推理是將因果推理應用於編碼科學知識的非常有代表性的研究。每一個結構化方程都決定了每一個反事實語句的真值。因此，我們可以解析地確定關於語句真實性的概率是不是可以從實驗或觀察研究（或實驗加觀察）中進行估計（Balke and Pearl, 1994; Pearl, 2000, Chapter 7）。

 

人們在因果論述中特別感興趣的是關注「效應的原因」的反事實問題（和「原因的效應」相對）。（Pearl，2015）

 

 

4. 調解分析和直接、間接效應的評估

 

調解分析關心的是將變化從原因傳遞到效應的機制。對中間機制的檢測是生成解釋的基礎，且必須應用反事實邏輯幫助進行檢測。反事實的圖形表徵使我們能定義直接和間接效應，並確定這些效應可從數據或實驗中評估的條件（Robins and Greenland, 1992; Pearl, 2001; VanderWeele, 2015）

 

5. 外部效度和樣本選擇偏差

 

每項實驗研究的有效性都需要考慮實驗和現實設置的差異。不能期待在某個環境中訓練的模型可以在環境改變的時候保持高性能，除非變化是局域的、可識別的。上面討論的 do-calculus 提供了完整的方法論用於克服這種偏差來源。它可以用於重新調整學習策略、規避環境變化，以及控制由非代表性樣本帶來的偏差（Bareinboim and Pearl, 2016）。

 

6. 數據丟失

 

數據丟失的問題困擾着實驗科學的所有領域。回答者不會在調查問卷上填寫所有的條目，傳感器無法捕捉環境中的所有變化，以及病人經常不知爲何從臨牀研究中突然退出。對於這個問題，大量的文獻致力於統計分析的黑箱模型範式。使用缺失過程的因果模型，我們可以形式化從不完整數據中恢復因果和概率的關係的條件，並且只要條件被滿足，就可以生成對所需關係的一致性估計（Mohan and Pearl, 2017）。

 

7. 挖掘因果關係

 

上述的 d-分離標準使我們能檢測和列舉給定因果模型的可測試推斷。這爲利用不精確的假設、和數據相容的模型集合進行推理提供了可能，並可以對模型集合進行緊湊的表徵。人們已在特定的情景中做過系統化的研究，可以顯著地精簡緊湊模型的集合，從而可以直接從該集合中評估因果問詢。

 

NIPS 2017 研討會 Q&A

 

我在一個關於機器學習與因果性的研討會（長灘 NIPS 2017 會議之後）上發表了講話。隨後我就現場若干個問題作了迴應。我希望從中你可以發現與博客主題相關的問題和回答。

 

一些人也想拷貝我的 PPT，下面的鏈接即是，並附上論文：

 

• http://ftp.cs.ucla.edu/pub/stat_ser/r475.pdf

   

• NIPS 17 – What If? Workshop Slides (PDF)（http://causality.cs.ucla.edu/blog/wp-content/uploads/2017/12/nips-dec2017-bw.pdf）

   

• NIPS 17 – What If? Workshop Slides (PPT [zipped])（http://causality.cs.ucla.edu/blog/wp-content/uploads/2017/12/nips-dec2017-bw.pdf）

   

問題 1：「因果革命」是什麼意思？

 

回答：「革命」是詩意用法，以總結 Gary King 的奇蹟般的發現：「在過去幾十年裏，對於因果推斷的瞭解比以前所有歷史記載的總和還要多」（參見 Morgan 和 Winship 合著的書的封面，2015）。三十年之前，我們還無法爲「Mud does not

 

cause Rain」編寫一個公式；現在，我們可以公式化和評估每一個因果或反事實陳述。

 

問題 2：由圖模型產生的評估與由潛在結果的方法產生的評估相同嗎？

 

回答：是的，假設兩種方法開始於相同的假設。圖方法（graphical approach）中的假設在圖中被展示，而潛在結果方法（potential outcome approach）中的假設則通過使用反事實詞彙被審查者單獨表達。

 

問題 3：把潛在的結果歸因於表格個體單元的方法似乎完全不同於圖方法中所使用的方法。它們的區別是什麼？

 

回答：只在有可條件忽略的特定假設成立的情況下，歸因纔有效。表格本身並未向我們展示假設是什麼，其意義是什麼？爲了搞明白其意義，我們需要一個圖，因爲沒有人可在頭腦中處理這些假設。流程上的明顯差異反映了對假設可見的堅持（在圖框架中），而不是使其隱藏。

 

問題 4：有人說經濟學家並不使用圖，因爲其問題不同，並且也沒能力建模整個經濟。你同意這種解釋嗎？

 

回答：不同意！從數學上講，經濟問題與流行病學家（或其他科學家）面臨的問題並無不同，對於後者來講，圖模型已經成爲了第二語言。此外，流行病學家從未抱怨圖迫使其建模整個人體解剖結構。（一些）經濟學家中的圖規避（graph-avoidance）是一種文化現象，讓人聯想到 17 世紀意大利教會天文學家避開望遠鏡。底線：流行病學家可以判斷他們的假設的合理性——規避掉圖的經濟學家做不到（我提供給他們很多公開證明的機會，並且我不責怪他們保持沉默；沒有外援，這個問題無法被處理）。

 

問題 5：深度學習不僅僅是盛讚曲線擬合？畢竟，曲線擬合的目標是最大化擬合，同時深度學習中很多努力也在最小化過擬合。

 

回答：在你的學習策略中不管你使用何種技巧來最小化過擬合或其他問題，你依然在優化已觀察數據的一些屬性，同時不涉及數據之外的世界。這使你立即回到因果關係階梯的第一階段，其中包含了第一階段要求的所有限制。

 

原文鏈接：http://causality.cs.ucla.edu/blog/index.php/2017/12/19/nips-2017-qa-follow-up/