機器學習——特徵工程

摘要： 特徵工程，是對原始數據進行一系列的工程處理，將其提煉為特徵，作為輸入供算法和模型使用。特徵工程是一個表示和展現數據的過程。在實際工作中，特徵工程主要是去除原始數據中的雜質和冗餘，設計更高效的特徵以描述求解的問題和預測模型之間的關係。

對於機器學習問題，數據和特徵決定了結果的上限，模型和算法的選擇及優化則是在逐步靠近達到這個上限值。

特徵工程，是對原始數據進行一系列的工程處理，將其提煉為特徵，作為輸入供算法和模型使用。特徵工程是一個表示和展現數據的過程。在實際工作中，特徵工程主要是去除原始數據中的雜質和冗餘，設計更高效的特徵以描述求解的問題和預測模型之間的關係。

一、為什麼需要對數值類型的特徵做歸一化？

為了消除數據特徵之間的量綱影響，我們需要對特徵進行歸一化，使不同指標之間具有可比性。對數值類型的特徵做歸一化(normalization)可以將所有的特徵都統一到一個大致相同的區間內。最常用的歸一化方法有兩種：

1） 線型數據歸一化（Min-Max Scaling）。通過對原始數據進行線性變換，使結果映射到[0,1]之間。實現對原始數據的等比例縮放。歸一化公式為：

X_norm = (X - X_min) / (X_max - X_min)

其中，X為原始數據，X_max， X_min分別為數據集的最大值和最小值

2）另一種最常用的歸一化是零均值歸一化（z-score normalization），它會將特徵變換映射到以均值為0、標準差為1的正態分佈上。準確的來說，假設原始特徵的均值為μ、標準差為σ，那麼z-score normalization定義為：

Z = (x - μ)/σ

為什麼通常需要對數值型做歸一化呢？我們可以藉助隨機梯度下降來說明歸一化的重要性。假設有兩種數值型特徵，x1的取值範圍為[0, 10]，x2的取值範圍為[0, 3]，可以構造一個目標函數符合以下等值圖：

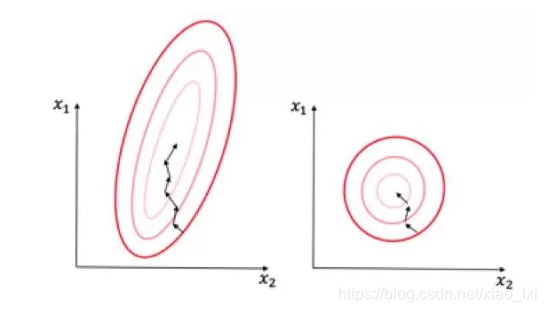
在學習速率相同的情況下，x1的更新速度會大於x2，需要更多的迭代才能找到最優值[1]。如果將x1和x2歸一化到相同的區間後，則優化目標的等值圖會變成右圖的圓形，x1和x2的更新速度會比較一致，能夠更快的找到最優值。

那麼歸一化適用於哪些模型，又對哪些模型是不適用的呢？首先，通過梯度下降法求解的模型是需要歸一化的，包括包括線性回歸、logistic regression、支持向量機(Support Vector Machine)、神經網絡(Neuro Network)。但對於決策樹模型則是不適用的，以C4.5為例，決策樹在進行節點分裂時主要依據的是x >= threshold 和x < threshold的信息增益比，而信息增益比跟x是否經過歸一化是無關的，因為歸一化並不會改變樣本在x上的相對順序。

二、怎樣處理類別型特徵？

類別型特徵(categorical feature)主要是指性別(男、女)、血型(A、B、AB、O)等類似的在有限選項內取值的特徵。通常類別型特徵原始輸入都是字符串形式，只有決策樹等少數模型能直接處理字符串形式的輸入。對於Logistic Regression、線性支持向量機等模型來說，類別型特徵必須經過處理轉換成數值型特徵才能正確工作。

此處主要介紹三種常用的轉換方法：Ordinal Encoding、One-hot Encoding、Binary Encoding。

Ordinal Encoding、One-hot Encoding、Binary Encoding。

Ordinal Encoding（序號編碼）通常用於處理類別間具有大小關係的數據，例如成績可以分為Low、Medium、High三檔，並且存在High > Medium > Low的排序關係。 Ordinal Encoding會按照大小關係對類別型特徵賦予一個數值ID，例如High表示為3、Medium表示為2、Low表示為1，轉換後依然保留了大小關係。

One-hot Encoding（獨熱編碼）通常用於處理類別間不具有大小關係的特徵，以血型為例，血型一共有四個取值(A、B、AB、O)，在One-hot Encoding後血型會變成一個4維稀疏向量：A型血表示為(1, 0, 0, 0)，B型血表示為(0, 1, 0, 0)，AB型表示為(0, 0, 1 , 0)，O型血表示為(0, 0, 0, 1)。對於類別取值較多的情況下使用One-hot Encoding需要注意以下問題： 使用稀疏向量來節省空間：在One-hot Encoding下，只有某一維取值為1，其他位置取值均為0。因此可以用向量的稀疏表示來有效節省空間，並且目前大部分的算法都會實現接受稀疏向量形式的輸入。

配合特徵選擇來降低維度：高維度特徵會帶來兩方面的問題：(1)在K近鄰算法中，高緯空間下兩點之間的距離很難得到有效的衡量; (2) 在Logistic Regression中，模型的參數的數量會隨著維度的增高而增加，容易引起過擬合問題; (3) 通常只有部分維度是對分類、預測有幫助，因此可以考慮配合特徵選擇來降低維度。

最後介紹Binary Encoding（二進制編碼），該方法主要分為兩步：用Ordinal Encoding給每個類別賦予一個ID，然後將ID對應的二進制編碼作為結果。以血型A、B、AB、O為例，Binary Encoding的過程如下圖所示：A型血的Ordinal Encoding為1，二進製表示為(0, 0, 1)；B型血的Ordinal Encoding為2，二進製表示為(0, 1, 0)，以此類推可以得到AB型血和O型血的二進製表示。可以看出，Binary Encoding本質上是利用二進制編碼對ID進行哈希，最終得到了0/1向量維數要少於One-hot Encoding，節省了空間。

除了本章介紹的Encoding方法外，還有其他的編碼方式，包括Helmert Contrast、Sum Contrast、Polynomial Contrast、Backward Difference Contrast。

三、怎樣處理高維組合特徵？

為了提高複雜關係的擬合能力，在特徵工程中經常會把一階離散特徵兩兩組合成高階特徵，構成交互特徵（Interaction Feature）。以廣告點擊預估問題為例，如圖1所示，原始數據有語言和類型兩種離散特徵。為了提高擬合能力，語言和類型可以組成二階特徵，如圖2所示：

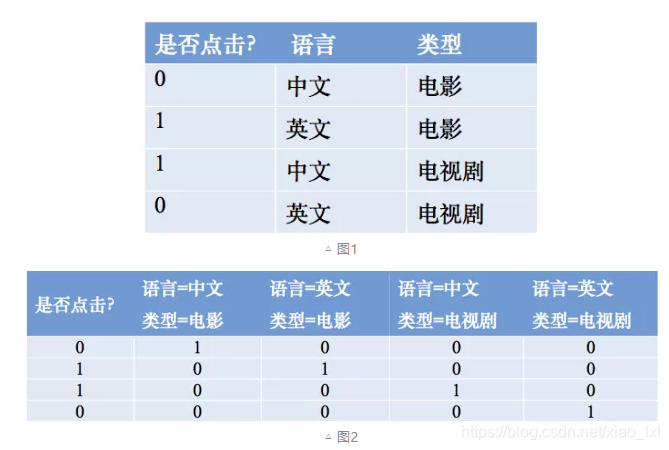
以Logistic Regression為例，假設數據的特徵向量X = (x_1, x_2, …, x_k)，我們有

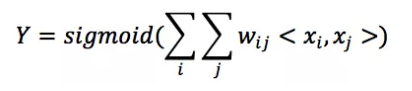
其wij的維度等於|xi| * |xj|。在上面的廣告點擊預測問題當中，w的維度是4（2x2，語言取值為中文或者英文、 類型的取值為電影或者電視劇）。 在上面廣告預測的問題看起來特徵組合是沒有任何問題的，但當引入ID類型的特徵時，問題就出現了。以推薦問題為例，原始數據如圖3所示，用戶ID和物品ID組合成新的特徵後的數據如圖4所示：

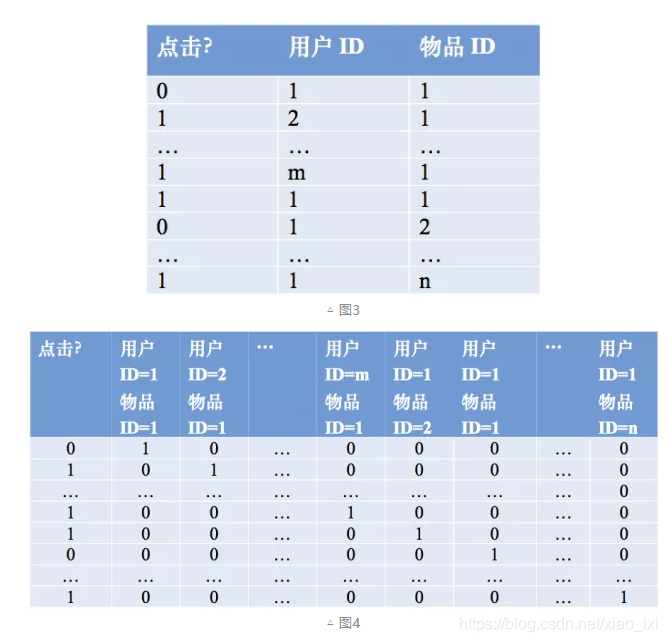
假設用戶的數量為m、物品的數量為n，那麼需要學習的參數的規模為m × n。在互聯網環境下，用戶數量和物品數量都可以到達千萬量級，幾乎無法學習m × n的參數規模。在這種情況下，一種行之有效的方法是將用戶和物品分別用k維的低維向量表示(k << m, k << n)，

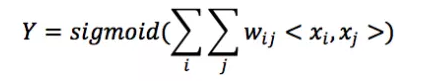
其中wij＝xi’ · xj’，在這裡xi’和xj’分別表示對應的低維向量。在上面的推薦問題中，需要學習的參數的規模為m × k + n × k。熟悉推薦算法的同學可以看出來這等於矩陣分解，希望這篇文章提供了另一個理解矩陣分解的思路。

四、怎樣有效地找到組合特徵？

在上節中我們介紹瞭如何利用降維方法來減少兩個高維特徵進行組合需要學習的參數。但是在很多實際數據當中，我們常常需要面對多種高維特徵。如果簡單的兩兩組合，參數過多、容易過擬合的問題依然存在，並且並不是所有的特徵組合都是有意義地。因此，我們迫切需要一種有效地方法來幫助我們找到哪些特徵應該進行組合。

本節介紹介紹一種基於決策樹的特徵組合尋找方法[3]。以點擊預測問題為例，假設原始輸入特徵包含年齡、性別、用戶類型（試用期、付費）、物品類型（護膚、食品等）四個方面的信息，並且假設我們根據原始輸入和標籤（點擊與否）構造出了兩個決策樹，那麼每一條從根節點到葉子節的路徑都可以看成一種特徵組合的方式。具體來說，我們可以將“年齡<=35”且“性別=女”看成一個特徵組合，將“年齡<=35”且“物品類別＝護膚”看出是一個特徵組合，將“用戶類型＝付費”且“物品類型＝食品”看成是一種特徵組合，將“用戶類型＝付費”且“年齡<=40”看成是一種特徵組合。假設我們有兩個樣本如下表所示，那麼第一行可以編碼為(1, 1, 0, 0)，因為既滿足“年齡<=35”且“性別=女”，也滿足“年齡<= 35”且“物品類別＝護膚”。同理可以看出第二個樣本可以編碼為(0, 0, 1, 1)，因為既滿足“用戶類型＝付費”且“物品類型＝食品”，又滿足“用戶類型＝付費”且“年齡<=40”。

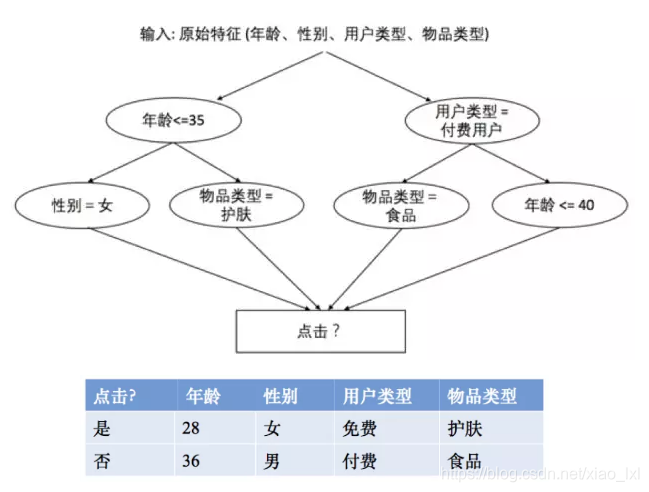
最後，那麼給定原始輸入該如何有效構造多棵決策樹呢？在這裡我們採用梯度提升決策樹 (gradient boosting decision tree)，該方法地思想是每次都在之前構建的決策樹的殘差(residual)上構建下一棵決策樹。

原文鏈接： CDSN

版权声明：本文為CSDN博主「Nani_xiao」的原創文章，遵循 CC 4.0 by-sa 版权协议，转载请附上原文出处链接和本声明。

若喜歡本文，請關注我們的臉書 Please Like our Facebook Page： Big Data In Finance