機器學習常用的奇異值分解的是什麼？

奇異值分解（簡稱SVD）用途非常廣泛。本文簡述SVD重點並舉一例說明分解式的計算步驟。

設 A 為一個 m X n 階實矩陣，r=rank A，SVD 具有以下形式：

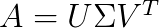
其中 U 是 m X m 階，V 是 n X n 階，Σ 是 m X n 階。特別的是，方陣 U 和 V 都是實正交矩陣 (orthogonal matrix)，也就是說，

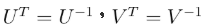
，Σ 是 (類) 對角矩陣，如下：

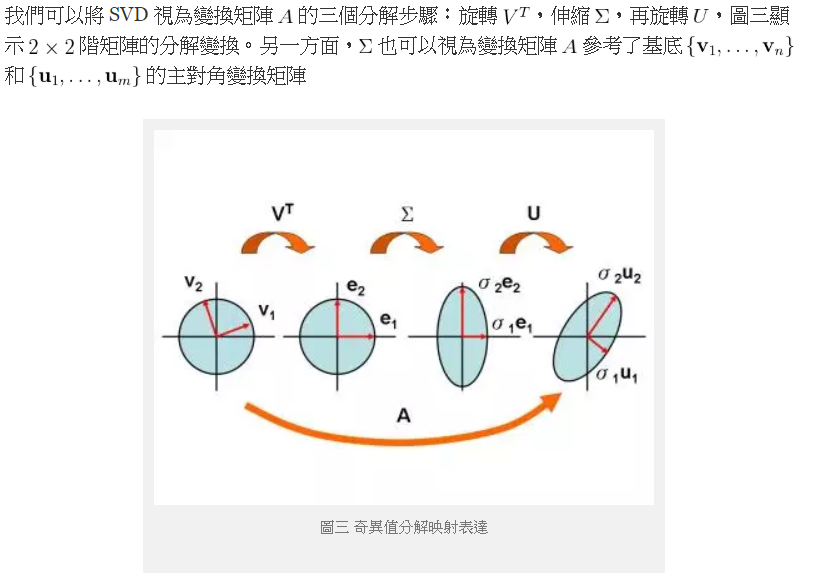
利用圖示可以幫助我們了解 SVD 的矩陣結構。SVD 最特別的地方是 \Sigma 的多數元為零，圖一的白色區塊以及黃色區塊的非對角元皆為零。

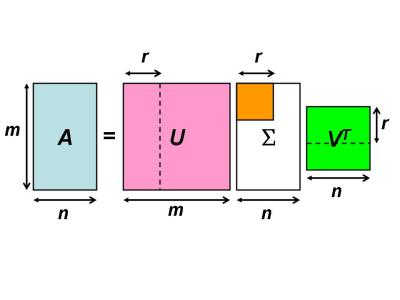
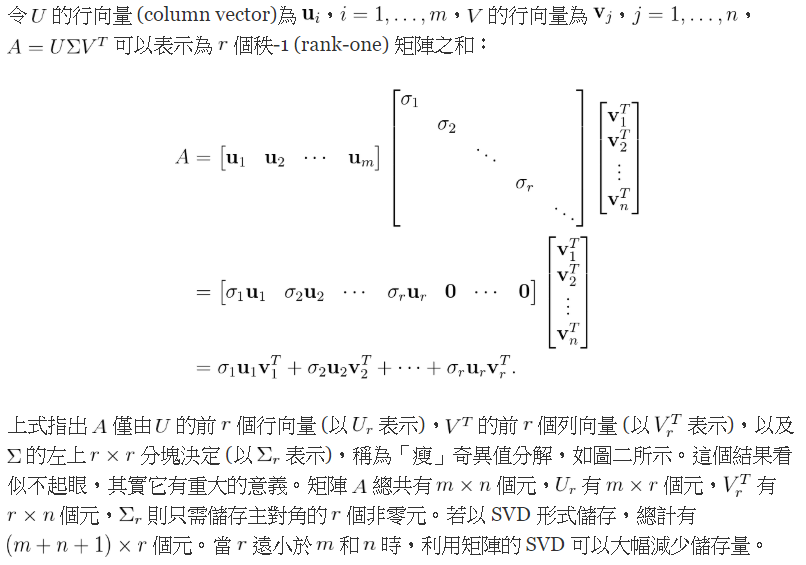
SVD 的計算主要是利用下面幾個性質：

底下舉一個例說明奇異值分解計算程序。考慮 4 X 5 階矩陣

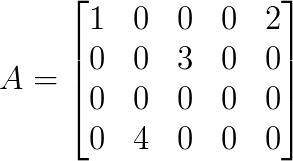
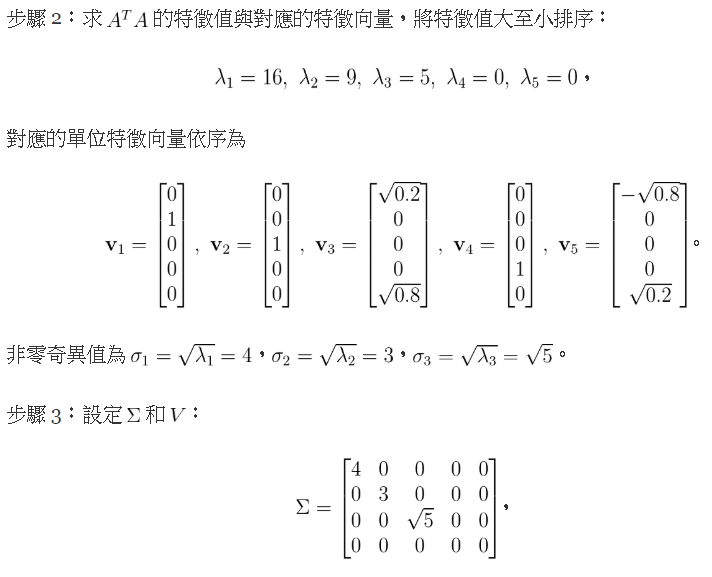
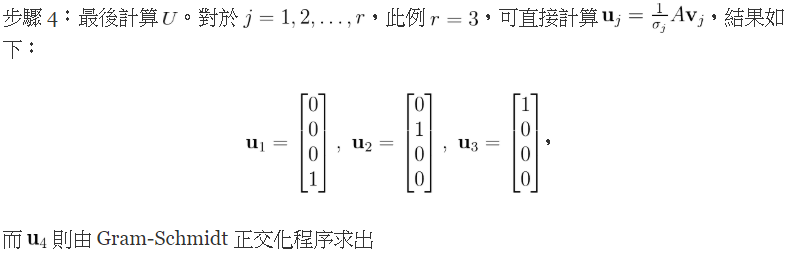
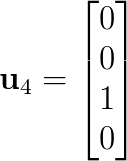
合併上面結果，

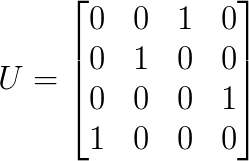
轉貼自： 線代啟示錄

若喜歡本文，請關注我們的臉書 Please Like our Facebook Page： Big Data In Finance