摘要: 粒子群算法(Particle swarm optimization,PSO)是模擬群體智能所建立起來的一種優化算法,主要用於解決最優化問題(optimization problems)。 1995年由 Eberhart和Kennedy 提出,是基於對鳥群覓食行為的研究和模擬而來的。
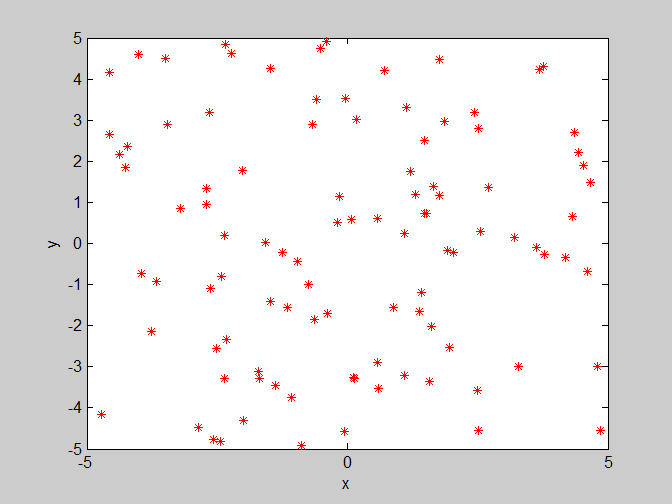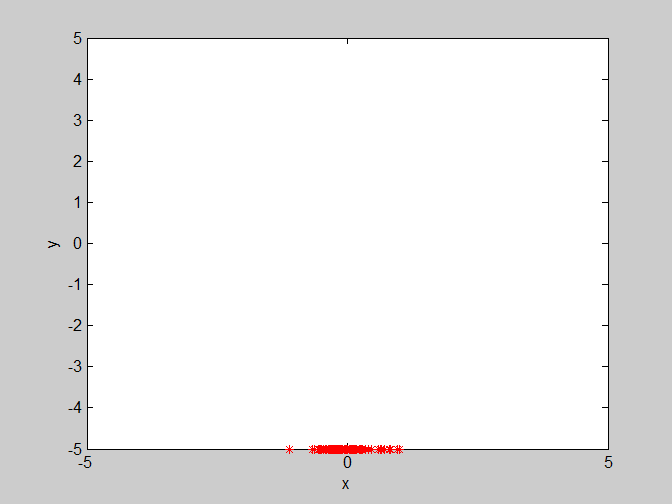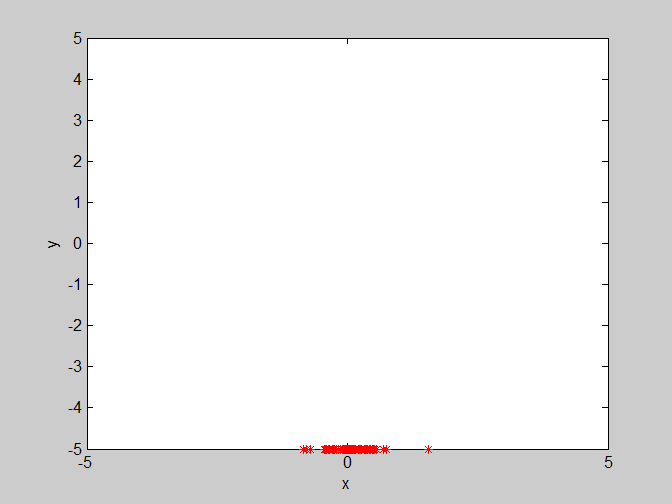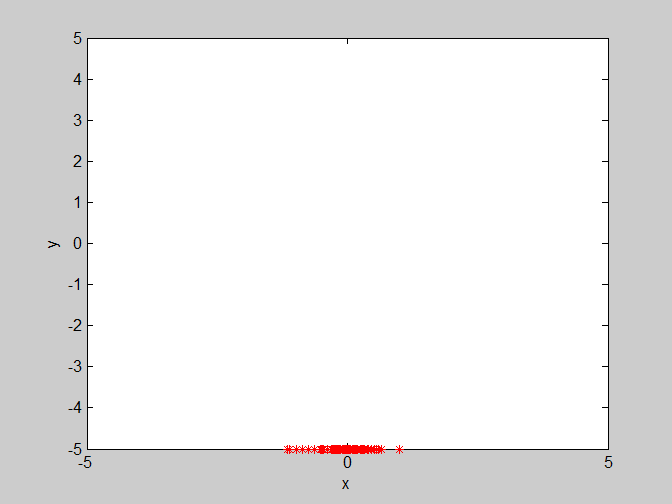
假設一群鳥在覓食,在覓食範圍內,只在一個地方有食物,所有鳥兒都看不到食物(即不知道食物的具體位置。當然不知道了,知道了就不用覓食了) ,但是能聞到食物的味道(即能知道食物距離自己是遠是近。鳥的嗅覺是很靈敏的)。
假設鳥與鳥之間能共享信息(即互相知道每個鳥離食物多遠。這個是人工假定,實際上鳥們肯定不會也不願意),那麼最好的策略就是結合自己離食物最近的位置和鳥群中其他鳥距離食物最近的位置這2個因素綜合考慮找到最好的搜索位置。 粒子群算法與《遺傳算法》等進化算法有很多相似之處。也需要初始化種群,計算適應度值,通過進化進行迭代等。但是與遺傳算法不同,它沒有交叉,變異等進化操作。與遺傳算法比較,PSO的優勢在於很容易編碼,需要調整的參數也很少。
一、基本概念
與遺傳算法類似,PSO也有幾個核心概念。
1. 粒子(particle):一只鸟。类似于遗传算法中的个体。
2. 種群(population):一群鳥。類似於遺傳算法中的種群。
3. 位置(position):一個粒子(鳥)當前所在的位置。
4. 經驗(best):一個粒子(鳥)自身曾經離食物最近的位置。
5. 速度(velocity ):一個粒子(鳥)飛行的速度。
6. 適應度(fitness):一個粒子(鳥)距離食物的遠近。與遺傳算法中的適應度類似。
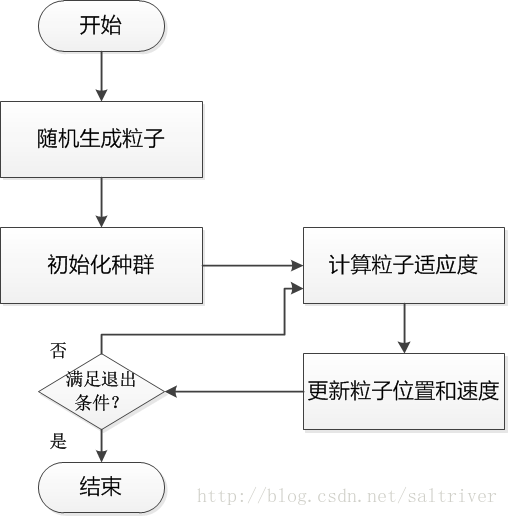
二、粒子群算法的過程
可以看出,粒子群算法的過程比遺傳算法還要簡單。
1. 根據問題需要,隨機生成粒子,粒子的數量可自行控制。
2. 將粒子組成一個種群。這前2個過程一般合併在一起。
3. 計算粒子適應度值。
4. 更新種群中每個粒子的位置和速度。
5. 速度(velocity ):一個粒子(鳥)飛行的速度。
6. 滿足退出條件就退出,不滿足就轉向步驟3
三、核心—“速度更新”
從上面PSO的算法流程中可以看出,核心步驟是更新種群中每個粒子的位置和速度,而速度的更新又是核心中的核心。 下面直接給出速度更新公式:
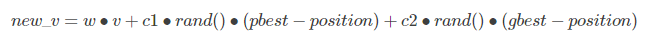
v為粒子當前的速度,w為慣性因子(有速度就有運動慣性)。 rand()為隨機數生成函數,能夠生成0-1之間的隨機數。 position為粒子當前的位置,pbest為本粒子歷史上最好的位置,gbest為種群中所有粒子中當前最好的位置。 c1和c2表示學習因子,分別向本粒子歷史最好位置和種群中當前最好位置進行學習。
參數好像也有很多,需要設置的是3個,w,c1和c2,但實際上一般都設置c1=c2=1,w一般設在0.5左右。所以也沒什麼好設置的。
從物理原理上來解釋這個速度更新公式,該公式由加號分割為3個部分:
第一部分是慣性保持部分,粒子沿著當前的速度和方向慣性飛行,不會偏移,直來直去。 (牛頓運動學第一定理)。
第二部分是自我認知部分,粒子受到自身歷史最好位置的吸引力,有回到自身歷史最好位置的意願。 (牛頓運動學第二定理)。
第三部分是社會認知部分,粒子處在一個社會中(種群中),社會上有更好的粒子(成功人士),粒子受到成功人士的吸引力,有去社會中成功人士位置的意願。 (牛頓運動學第二定理)。
速度更新公式的意義就是粒子在自身慣性和2種外力作用下,速度和方向發生的改變。
注意這3部分都有重要含義。沒有慣性部分,粒子們將很快向當前的自身最優位置和全局最優粒子位置靠攏,變成了一個局部算法了。有了慣性,不同粒子將有在空間中自由飛行的趨勢,能夠在整個搜索區域內尋找食物(最優解)。而沒有自我認知部分,粒子們將向當前的全局最優粒子位置靠攏,容易陷入局部最優。沒有社會認知部分,粒子們各自向自身最優位置靠攏,各自陷入自身最優,整個搜索過程都不收斂了。
最后,有了速度更新公式,位置更新就简单了:
new_position = position + new_v * t
t一般默认取1
原文鏈接: CDSN
版权声明:本文為CSDN博主「saltriver」的原創文章,遵循 CC 4.0 by-sa 版權協議,,轉載請附上原文出處鏈接及本聲明。
若喜歡本文,請關注我們的臉書 Please Like our Facebook Page: Big Data In Finance


留下你的回應
以訪客張貼回應