摘要: 近日南洋理工大學研究者發佈了一篇描述卷積網絡數學原理的論文,該論文從數學的角度闡述整個卷積網絡的運算與傳播過程。該論文對理解卷積網絡的數學本質非常有幫助,有助於讀者「徒手」(不使用卷積API)實現卷積網絡。
徒手實現CNN:綜述論文詳解卷積網絡的數學本質
近日南洋理工大學研究者發佈了一篇描述卷積網絡數學原理的論文,該論文從數學的角度闡述整個卷積網絡的運算與傳播過程。該論文對理解卷積網絡的數學本質非常有幫助,有助於讀者「徒手」(不使用卷積API)實現卷積網絡。
論文地址:https://arxiv.org/pdf/1711.03278.pdf
在該論文中,我們將從卷積架構、組成模塊和傳播過程等方面瞭解卷積網絡的數學本質。讀者可能對卷積網絡具體的運算過程比較瞭解,入門讀者也可先查看 Capsule 論文解讀的第一部分了解詳細的卷積過程,但其實我們一般並不會關注於卷積網絡到底在數學上是如何實現的。因爲各大深度學習框架都提供了簡潔的卷積層API,所以我們不需要數學表達式也能構建各種各樣的卷積層,我們最多隻需要關注卷積運算輸入與輸出的張量維度是多少就行。這樣雖然能完美地實現網絡,但我們對卷積網絡的數學本質和過程仍然不是太清楚,這也就是本論文的目的。
下面我們將簡要介紹該論文的主體內容,並嘗試理解卷積網絡的數學過程。有基礎的讀者可以查閱原論文以實現更深的理解,此外我們也許能借助該論文的計算式在不使用層級 API 的情況下實現簡單的卷積網絡。

卷積神經網絡(CNN)或稱爲 ConvNet 廣泛應用於許多視覺圖像和語音識別等任務。在 2012 ImageNet 挑戰賽 krizhevsky 等人首次應用深度卷積網絡後,深度卷積神經網絡的架構設計已經吸引了許多研究者做出貢獻。這也對深度學習架構的搭建產生了很重要的影響,如 TensorFlow、Caffe、Keras、MXNet 等。儘管深度學習的實現可以通過框架輕易地完成,但對於入門者和從業者來說,數學理論和概念是非常難理解的部分。本論文將嘗試概述卷積網絡的架構,並解釋包含激活函數、損失函數、前向傳播和反向傳播的數學推導。在本文中,我們使用灰度圖作爲輸入信息圖像,ReLU 和 Sigmoid 激活函數構建卷積網絡的非線性屬性,交叉熵損失函數用於計算預測值與真實值之間的距離。該卷積網絡架構包含一個卷積層、池化層和多個全連接層。
2 架構
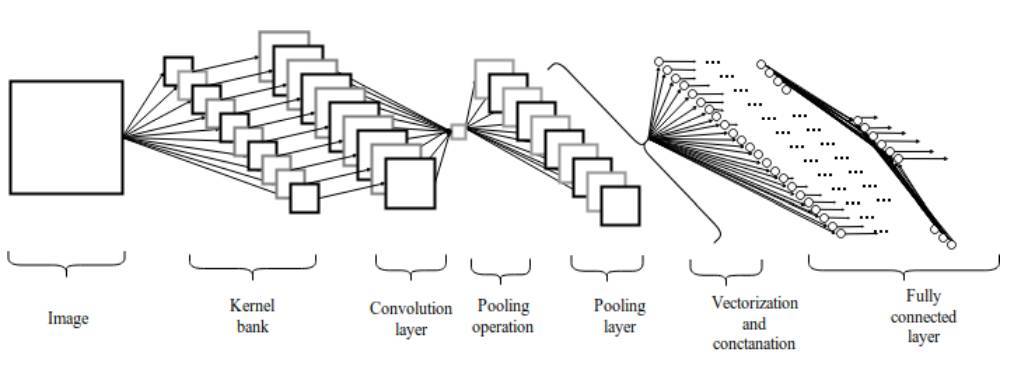
圖 2.1:卷積神經網絡架構
2.1 卷積層
卷積層是一組平行的特徵圖(feature map),它通過在輸入圖像上滑動不同的卷積核並執行一定的運算而組成。此外,在每一個滑動的位置上,卷積核與輸入圖像之間會執行一個元素對應乘積並求和的運算以將感受野內的信息投影到特徵圖中的一個元素。這一滑動的過程可稱爲步幅 Z_s,步幅 Z_s 是控制輸出特徵圖尺寸的一個因素。卷積核的尺寸要比輸入圖像小得多,且重疊或平行地作用於輸入圖像中,一張特徵圖中的所有元素都是通過一個卷積覈計算得出的,也即一張特徵圖共享了相同的權重和偏置項。
然而,使用較小尺寸的卷積核將導致不完美的覆蓋,並限制住學習算法的能力。因此我們一般使用 0 填充圖像的四周或 Z_p 過程來控制輸入圖像的大小。使用 0 填充圖像的四周 [10] 也將控制特徵圖的尺寸。在算法的訓練過程中,一組卷積核的維度一般是(k_1, k_2, c),這些卷積核將滑過固定尺寸的輸入圖像(H, W, C)。步長和 Padding 是控制卷積層維度的重要手段,因此產生了疊加在一起形成卷積層的特徵圖。卷積層(特徵圖)的尺寸可以通過以下公式 2.1 計算。
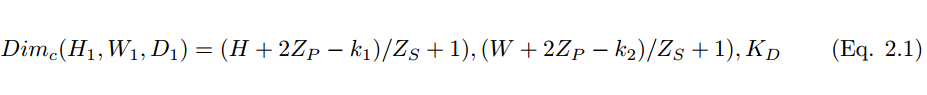
其中 H_1、W_1 和 D_1 分別爲一張特徵圖的高度、寬度和深度,Z_p 爲 Padding 、Z_s 爲步幅大小。
2.2 激活函數
激活函數定義了給定一組輸入後神經元的輸出。我們將線性網絡輸入值的加權和傳遞至激活函數以用於非線性轉換。典型的激活函數基於條件概率,它將返回 1 或 0 作爲輸出值,即 op {P(op = 1|ip) or P(op = 0|ip)}。當網絡輸入信息 ip 超過閾值,激活函數返回到值 1,並傳遞信息至下一層;如果網絡輸入 ip 值低於閾值,它返回到值 0,且不傳遞信息。基於相關信息和不相關信息的分離,激活函數決定是否應該激活神經元。網絡輸入值越高,激活越大。不同類型的激活函數應用各異,一些常用的激活函數如表 1 所示。
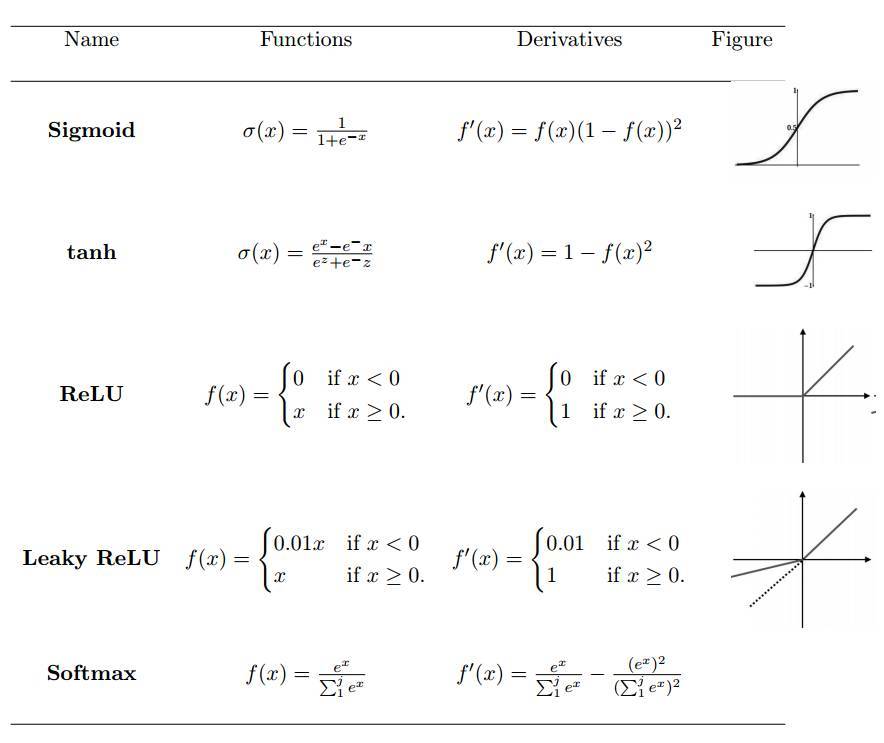
表1:非線性激活函數
2.3 池化層
池化層是指下采樣層,它把前層神經元的一個集羣的輸出與下層單個神經元相結合。池化運算在非線性激活之後執行,其中池化層有助於減少參數的數量並避免過擬合,它同樣可作爲一種平滑手段消除不想要的噪音。目前最常見的池化方法就是簡單的最大池化,在一些情況下我們也使用平均池化和 L2 範數池化運算。
當採用卷積核的數量 D_n 和步幅大小 Z_s 用來執行池化運算,其維度可通過下式被計算:
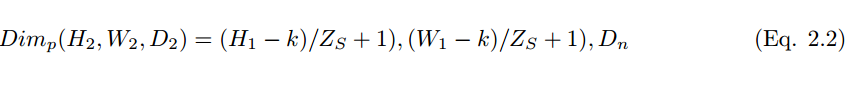
2.4 全連接層
池化層之後,三維像素張量需要轉換爲單個向量。這些向量化和級聯化的數據點隨後會被饋送進用於分類的全連接層。全連接層的函數即特徵的加權和再加上偏置項並饋送到激活函數的結果。卷積網絡的架構如圖 2 所示。這種局部連接類的架構在圖像分類問題上 [11] [12] 超越傳統的機器學習算法。
2.5 損失或成本函數
損失函數將一個或多個變量的事件映射到與某個成本相關的實數上。損失函數用於測量模型性能以及實際值 y_i 和預測值 y hat 之間的不一致性。模型性能隨着損失函數值的降低而增加。
如果所有可能輸出的輸出向量是 y_i = {0, 1} 和帶有一組輸入變量 x = (xi , x2 . . . xt) 的事件 x,那麼 x 到 y_i 的映射如下:
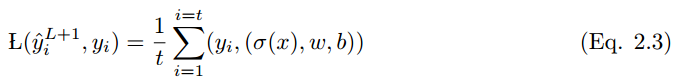
其中 L(y_i hat , y_i) 是損失函數。很多類型的損失函數應用各不相同,下面給出了其中一些。
2.5.1 均方誤差
均方誤差或稱平方損失函數多在線性迴歸模型中用於評估性能。如果 y_i hat 是 t 個訓練樣本的輸出值,y_i 是對應的標籤值,那麼均方誤差(MSE)爲:
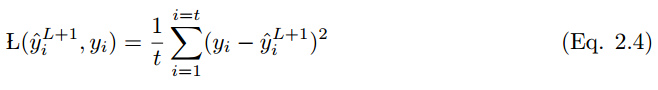
MSE 不好的地方在於,當它和 Sigmoid 激活函數一起出現時,可能會出現學習速度緩慢(收斂變慢)的情況。
這一部分描述的其它損失函數還有均方對數誤差(Mean Squared Logarithmic Error)、L_2 損失函數、L_1 損失函數、平均絕對誤差(Mean Absolute Error)、平均絕對百分比誤差(Mean Absolute Percentage Error)等。
2.5.7 交叉熵
最常用的損失函數是交叉熵損失函數,如下所示。如果輸出 y_i 在訓練集標籤 中的概率爲 ,輸出 y_i 不在訓練集標籤 的概率爲 。期望標籤爲 y,因此:
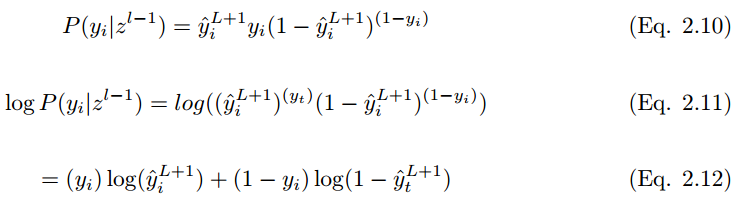
爲了最小化代價函數,
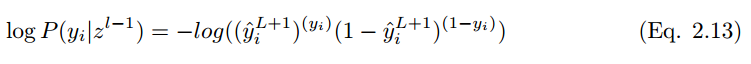
在 i 個訓練樣本的情況下,代價函數爲:
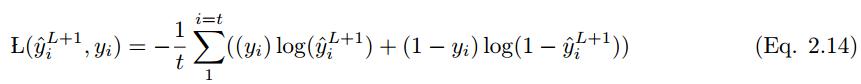
3 卷積網絡的學習
3.1 前饋推斷過程
卷積網絡的前饋傳播過程可以從數學上解釋爲將輸入值與隨機初始化的權重相乘,然後每個神經元再加上一個初始偏置項,最後對所有神經元的所有乘積求和以饋送到激活函數中,激活函數對輸入值進行非線性變換並輸出激活結果。
在離散的色彩空間中,圖像和卷積核可以分別表徵爲 (H, W, C) 和 (k_1, k_2, c) 的三維張量,其中 m、n、c 分別表示第 c 個圖像通道上第 m 行和第 n 列的像素。前兩個參數表示空間座標,而第三個參數表示色彩的通道。
如果一個卷積核在彩色圖像上滑動運算,那麼多維張量的卷積運算可以表示爲:
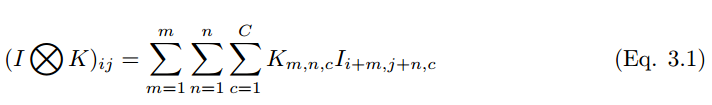
卷積過程可以用符號 ⓧ 表示。對於灰度標量圖來說,卷積過程可以表示爲,
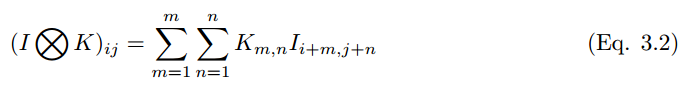
一個卷積核 (下文用 k_p,q|u,v 表示)滑動到圖像 I_m,n 的位置,其步幅爲 1 且帶有 Padding。那麼卷積層(下文用 C_p,q|m,n 表示)的特徵圖可以計算爲
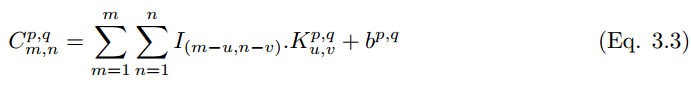
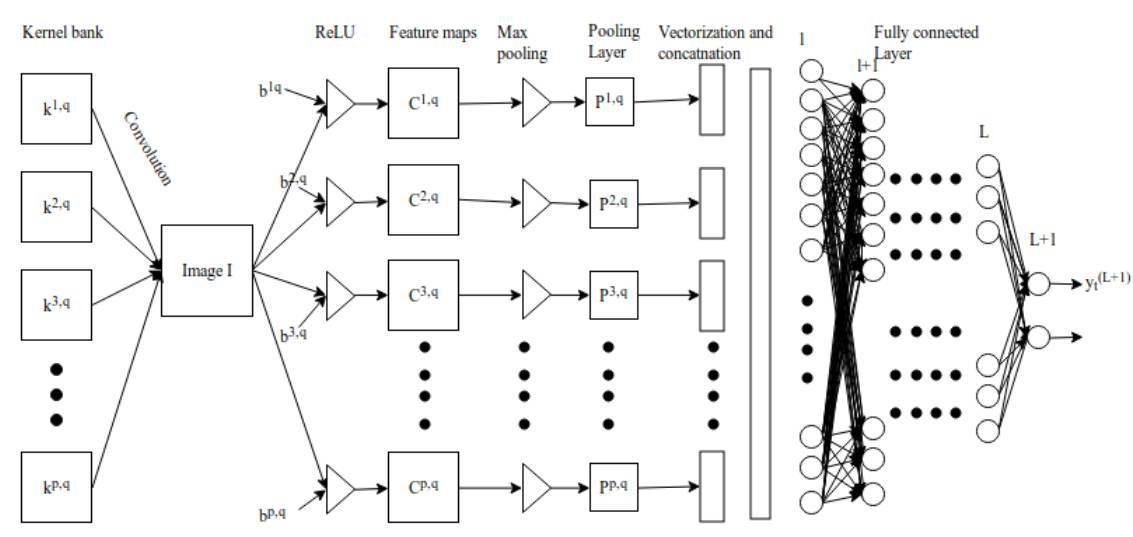
圖 3.1:卷積神經網絡
我們在執行卷積後需要使用非線性激活函數而得到特徵圖:
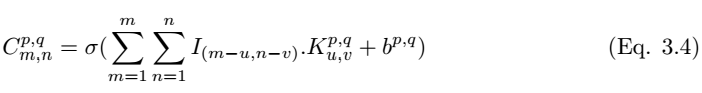
其中σ爲 ReLU 激活函數。池化層 P_p,q|m,n 可以通過選取卷積層中最大值的 m,n 來完成構建,池化層的構建可以寫爲,

池化層 P^p,q 的輸出可以級聯轉化爲一個長度爲 p*q 的向量,然後我們可以將該向量饋送到全連接網絡以進行分類,隨後 l-1 層向量化的數據點

可以通過以下方程計算:
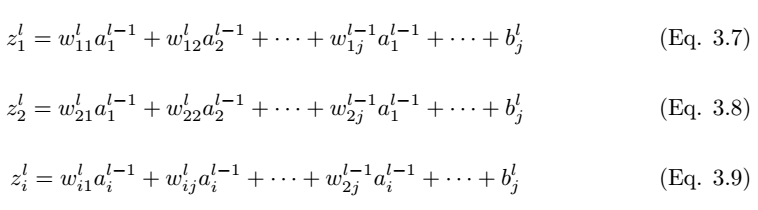
長向量從 l 層饋送到 L+1 層的全連接網絡。如果全連接層有 L 個、神經元有 n 個,那麼 l 可以表示第一個全連接層,L 表示最後一個全連接層,L+1 爲圖 3.2 展示的分類層,全連接層中的前向傳播過程可以表示爲:
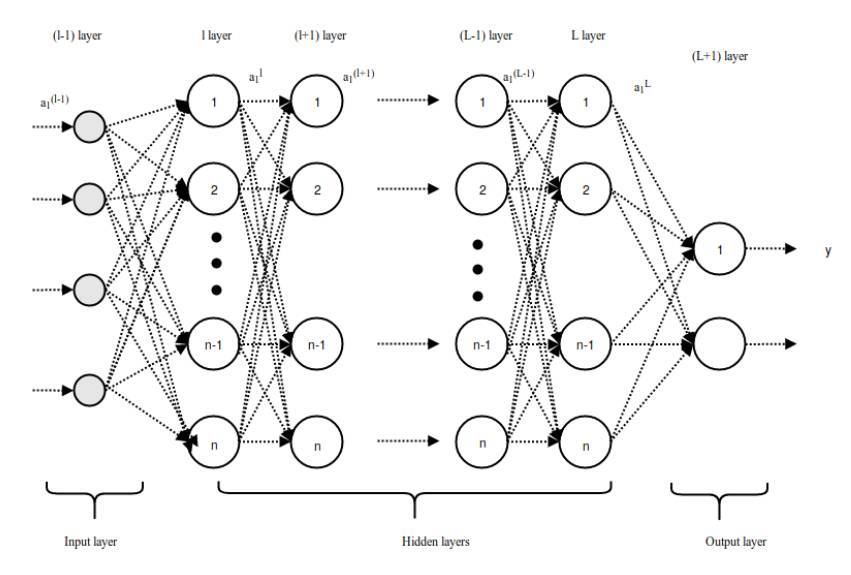
圖 3.2:全連接層中的前向傳播過程
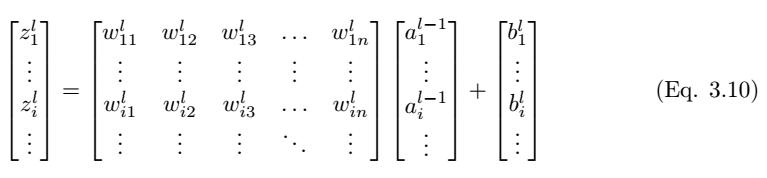
如圖 3.3 所示,我們考慮全連接層 l 中的單個神經元 (j)。輸入值 a_l-1,i 分別與權重 w_ij 求加權和並加上偏置項 b_l,j。然後我們將最後層的輸入值 z_l,i 饋送到非線性激活函數σ。最後層的輸入值可通過以下方程計算,
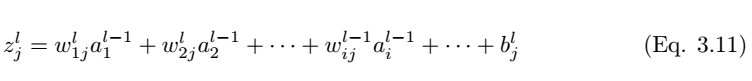
其中 z_l,i 爲 l 層中神經元 j 的激活函數的輸入值。
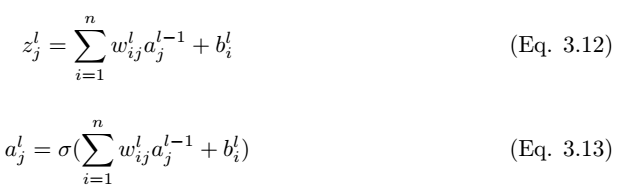
因此,第 l 層的輸出爲

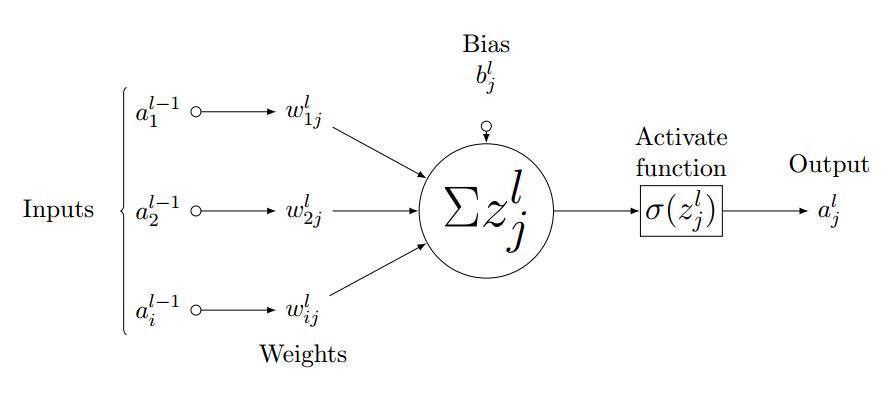
圖 3.3:第 l 層中神經元 j 的前向傳播過程

其中 a^l 是

W^l 是

同樣地,最後一層 L 的輸出值是

其中
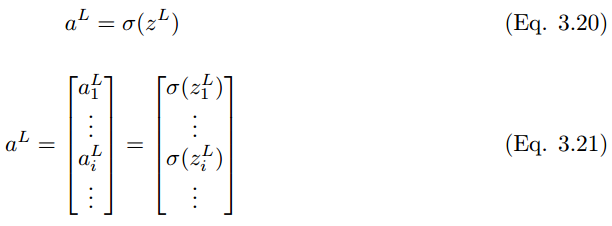
將這些擴展到分類層,則神經元單元 (i) 在 L + 1 層的最終輸出預測值 y_i hat 可以表示爲:
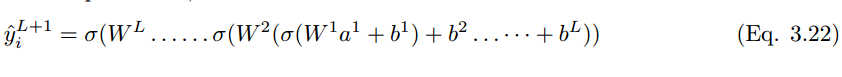
如果預測值是 y_i hat,實際標註值爲 y_i,那麼該模型的性能可以通過以下損失函數方程來計算。根據 Eqn.2.14,交叉熵損失函數爲:
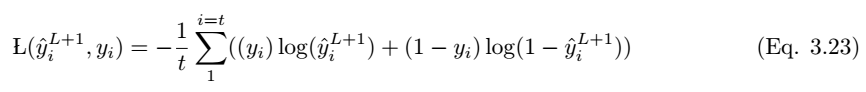
以上就是正向傳播的簡要數學過程,本論文還着重介紹了反向傳播的數學過程,不過限於篇幅我們並不在本文中展示,感興趣的讀者可以查閱原論文。
4 結語
本文通過概述對卷積神經網絡架構作出瞭解釋,其中包括不同的激活函數和損失函數,同時詳細解釋了前饋與反向傳播的各個步驟。出於數學簡明性的考慮,我們以灰度圖像作爲輸入信息。卷積核步長值取 1,使用 Padding。中間層和最後層的非線性轉換通過 ReLU 和 sigmoid 激活函數完成。交叉熵損失函數用來測量模型的性能。但是,需要大量的優化和正則化步驟以最小化損失函數,增加學習率,避免模型的過擬合。本文試圖只考慮帶有梯度下降優化的典型卷積神經網絡架構的制定。
轉貼自: 幫趣


留下你的回應
以訪客張貼回應