
1. 羅吉斯迴歸
羅吉斯迴歸對於預測二元分類的資料一直是非常實用的方法,且最大優點是對於預測結果具有解釋變數關係的能力,對於觀察因子的重要性及其中的隱含意義非常有幫助,透過迴歸及非線性轉換的概念,擬合出足以進行分類的模型,不論是學術上亦或是實務上都非常常見,藉由預先定義好的被解釋變數資料(Y),以及具有相關性的變數進行作為解釋變數(X),進行羅吉斯迴歸的訓練,便可以輕鬆得出足以預測泡沫發生的模型:
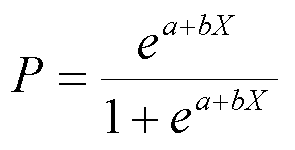
但使用羅吉斯迴歸最大的問題點在於如何定義泡沫的發生,過去對於泡沫的定義也未有較為統一的方式,一則較為簡單的方式為利用平均報酬減去3個標準差的,也可利用方法較為複雜的泡沫檢定GSADF去進行定義,究竟何種定義方式較好,則取決於投資者對於風險的容忍程度。
2. 類神經網路
近幾年,大數據及AI技術對於產業應用的發展日益成熟,而其中最為火熱的便是類神經網絡及其所延伸的深度學習,其核心概念是透過經多次非線性轉換的迴歸分析,去擬合出預測模型,由於經過多次非線性轉換的因素,雖然較無法解釋變數如何影響預測結果,但對於預測能力有顯著的提升,而類神經網路與羅吉斯回歸一樣,需要有預先定義好的泡沫定義,才能夠進行模型訓練及預測,但相較於羅吉斯回歸,此種方式要小心模型於樣本內過於擬合的問題(overfitting),使得實際應用於預測時效果不如預期,必須平衡好訓練資料集及驗證資料集所得出的訓練準確度,此方法才能夠發揮出超乎預期的效益。
3. LPPL
LPPL為Johansen, Ledoit and Sornette (2000)所提出的對數週期冪次法則,其 理論模型基本假設以投資人理性預期作為出發點,認為金融市場投資者容易被周遭參與者意見所影響,使得投資人間互相模仿,趨於採用相同的投資策略,進而推升股價,而當複雜系統達到臨界點(critical point)時,是泡沫最有可能發生破裂的時刻,而其達成的效果也於後續Sornette(2000)的JLS模型及其他文獻獲得證實,LPPL 數值分析可以抓住資產價格在崩盤前對數週期的表現,作為是否產生泡沫的依據,假如產生泡沫,在未來就很有可能造成崩盤。
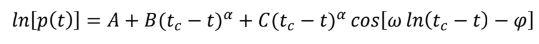
其中 p(t)為在 t 時間下的股價指數; tc>0 為泡沫結束日;0 < α < 1 為衡量價格上漲之加速度;ω 為量化對數週期振動頻率;0 < ψ < 2π為週期波動之初相位(phase)。由(3)式可知,LPPL 模型可由 3 個線性參數(A、B、C)與 4 個非線性參數(tc、α、ω、φ)來描述,參數之估計方法採用最小平方估計法(Least Squares Estimate):
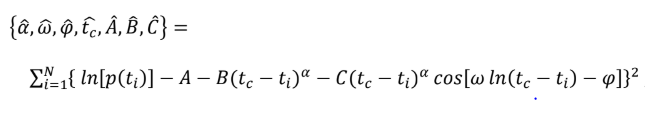
其中t(N) = t2,樣本時間點t ∈ [t1,t2]。若令yi = ln[p(ti)], fi = (tc − ti)^α , gi = (tc −ti)^α * cos[ω ln(tc − ti) − φ],則從一階條件(First Order Condition)中可得最佳解,投資者可藉由此模型預測泡沫崩跌時間點,以成功規避泡沫所造成的損失,也可配合前面所提到的羅吉斯回歸及類神經網路方法一同進行預測,獲得更加穩定的預測效果
本文內容參考自2015年科技部計畫 - 國際股市價格泡沫預測之研究:理論模型、實證分析應用與比較
若喜歡本文,請關注我們的臉書 Please Like our Facebook Page: Big Data In Finance


留下你的回應
以訪客張貼回應