本文重點:
為了更好的了解泡沫何時發生,我們首先要了解如何檢測,或者如何定義泡沫的發生。在以前的研究中已經有很多如何預測泡沫的方法,其中以Fas和理性泡沫模型最為著名,此處根據現有研究對這兩種模型進行詳細敘述。同時本文也敘述了檢測泡沫是否存在的方法GSADF,與傳統的ADF模型參照,該方法可以直接對資產價格進行檢驗,而無需計算基礎價格,能在檢測出爆炸性跑的同時實時檢測泡沫產生的時點。
一,Fads模型,該方法在Fama等(1988)和Culter等。 (1991)中被提出和採用。
p_t= p_t^* + e_t (1)
p_t^*= p_(t-1)^* + ϵ_t (2)
p_t:為第 t 期股票市價的對數
p_t^*:為第 t 期股市中非穩定之組成要件的對數
ϵ_t:為 white noise
傳統模型下對數變動價格是隨機漫步的,e_t=0 幷且報酬爲 white noise。由於p_t^*不包括FADS 的因子,因此將p_t^*視為基本價格。在 Fads模型下。價格有固定的組成:
e_t = ρ_u e_(t-1) + v_t (3)
Fads模型被定義爲σ_e^2 > 0和ρ_e > 0,其中σ_e^2為e_t的變異數。在股票價格中,穩定的組成要件??意味著報酬是可預期的。
Cutler et al.(1991)認為基期價格可以用逼近法衡量。由於這種逼近法可能會誤判,所以基本面模型幷沒有被普遍接受。采用變量誤差的方式對近似法進行建模:
P_t^f= p_t^* + w_t (4)
p^f:為近似值
w_t:為測量誤差(假設為連續且不相關)
Cutler et al.(1991)也提出以統計量 λ 作為反映測量誤差程度的方法
λ ≡ (σ_e^2)/([σ_e^2+σ_w^2]) (5)
若p^f能完美衡量基本面 (σ_w^2 = 0),則λ = 1。若p^f測量p^*有誤差,則λ < 1。在任何 情況下,由於λ為平方,故λ永遠為正的。
爲了瞭解 Fads 模型如何根據滯後的消息影響報酬的可預測性。使用式(1)至式(4)來表示基本面之近似值與對數變動價格之間報酬的差异。迴歸式如下:
p_(t+1) − p_t = β_0 + β_b(p_t − P_t^f) + v_(t+1) (6)
其中一個例子是基本面之近似值爲實際股息之對數(Cutler et al.(1991)在股票市場 收益的實證研究中使用的近似值)。式(6)爲滯後股利價格比對數之報酬迴歸式。
這就明顯意味著式(1)至式(4):

此 Fads 模型意味著β_b為負數。隨著 Fads 模型的擴展導致政體轉換之行爲。假設股票市場之收益的平方差隨著時間的推移而改變,則ε_t不是 white noise,而是異質性的。假設異質平方差具有: ε_(t+1)~?(0,σ_S) ???ℎ ??????????? ?
ε_(t+1)~?(0,σ_C) witℎ ??????????? 1 − ? (8)
σ_C > σ_S,因此 C 為高平方差之狀態,S 為低平方差之狀態。
Schwert(1989)提出了一種類似的異質平方差之公式。令函數型式q在0跟1 之間,採用對數模型如下:
q = ϕ(β_q0) (9)
ϕ:爲累積對數分布函數
β_q0:爲平均對數分布函數
Fads模型可以彙整為轉換迴歸式如下:
R_(S,t+1) = β_0 + β_b b_t + ε_(S,t+1)
R_(C,t+1) = β_0 + β_b b_t +ε_(C,t+1)
q = ϕ(β_q0) (10)
??:爲實質股票價格與基本面價格之偏差比例
上文參考自許銘仁(2018)《臺灣股市泡沫與其影響因素之研究》
二、 理性泡沫模型(Rational Bubble Model)
在理性泡沫模型的的假設之中,理性預期市成立的,當發生新的事件或情况時,交易者會預期其他交易者的預期結果,從而决定是否投資,因此産生投資的“共有信念”(Common Belief),當共有信念産生在加上市場中的投機性炒作,便産生泡沫。 假設在對稱信息下具有理性泡沫的存在,則所有代理人皆擁有理性預期的能力並且擁有相同的訊息。
由 Blanchard and Watson(1982)所提出的理性投機泡沫中,分爲確定型泡沫(Deterministic Bubbles)與隨機型泡沫(Stochastic Bubbles)兩種泡沫型態
(一) 確定型泡沫
E_t B_(t+1) = (1 + ?)B_t
確定型泡沫會隨著時間的增加而以指數的形式無限制的成長,而在現實環境中並不存在這種持續成長不會破滅的泡沫。
(二)隨機型泡沫 在隨機型泡沫下有兩種機制,分別爲以機率π與1 − π呈現。在機率π下,泡沫以(1 − r)/π的速度呈現指數成長;在機率1 − π下,泡沫會崩潰成為 White noise。
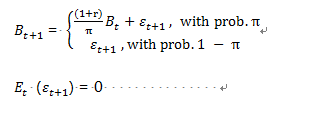
r 是從匯率模型所導出的常數,ϵ_t~???(0,σ_ϵ^2)。
E_t B_(t+1) = (1 + ?)B_t
考慮雙方的期望收益率,其中 E[.]為期望值,(1+r)為泡沫的預期成長率。隨機型泡沫的存續期間並不是無窮無盡的,隨機型泡沫的破滅可能性,會隨著泡沫的存續期間長短以及價格偏離市場基本面的程度而有所調整。泡沫的平均存續期間為〖(1 + π)〗^(-1)。
三,檢定泡沫存在的方法:廣義自回歸模型(GSADF)
GSADF由Phillips et al. 在2015年提出,是以單根檢定(ADF)為基礎所發展出來得進階泡沫檢定法。首先,先以單根檢定(ADF)來推導,並說明。 首先,對單根檢定(ADF)取最小上界值(SUP),並可以簡單定義為:
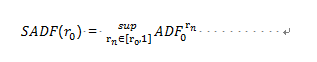
r_0是最小的樣本窗口寬度的分數(起始值),根據 Phillips et al. (PWY, 2015)文中,最小樣本窗口的算式為?0 = (0.01 + 1.8 √? )T,T 為總樣本數。式(3-14)表示單根檢定(ADF) 從 0 運行到r_n。SADF 是由 Phillips et al. (PWY, 2015)所提出,是根據向前遞歸的右尾單根檢定(ADF)的順序來檢定泡沫。但是,當樣本期間多次繁榮與崩潰時,PWY程序可能會因功率降低而受到影響,而無法檢定泡沫的存在。所以,SADF 在檢定長時間或擁有快速變化的市場數據時,可能檢定不出泡沫。
而廣義自回歸模型(GSADF)是以遞歸方式對數據樣本重複進行單根檢定(ADF)。也就是先以t_1為基期向後檢測,然後再以t_2為基期向後檢測,以此類推。我們假定GSADF在所有可行範圍內(r_1和r_2)的雙遞歸中最大的ADF統計量, 以 GSADF(r_0)表示。
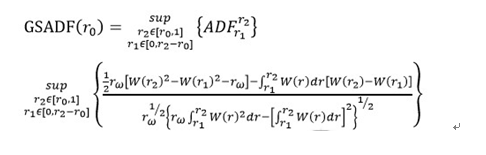
上式是 GSADF 檢驗統計量的極限分佈,r_ω = r_2 − r_1和 W 是標準 Wiener過程。在 PWY 中提出的策略是使用從樣本起始到的觀察值τ(展現在 I_(⌊T_r⌋)= {y_1, y_2,…, y_(T_r )}中的訊息)的數據進行右尾的遞歸ADF檢定。由於I_(⌊T_r⌋)可能包 含一個或多個崩潰的泡沫事件,所以這個ADF檢定與早期的單根檢定和基於協整的泡沫檢定一樣,可能導致偽靜態的行為。 而且,除了資料的第一個泡沫檢定成功,其他資料內的泡沫通常會檢定不出來。所以採用一種雙遞歸的檢定方式,稱為Backward Sup ADF,以提高泡沫識別的準確性。
Backward SADF 檢定就是對樣本序列進行反向的 sup ADF 檢定,其中每個樣本 的終值固定在r_2,並且從 0 開始變化到r_2 − r_0。BSADF 檢定就是固定最後一個窗口 的樣本作滾動窗口檢定。假設窗口設定 30,第一期的值,為樣本從 0 開始到 30 做一次 ADF 檢定;第二期的值,為樣本從 0 到 31 做一次 ADF 檢定,再從 1 到 31 做一次 ADF 檢定,
二者取其最大值為第二期的值。以此類推。表示成公式,如下:
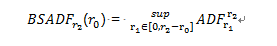
BSADF 提供了更多樣本的訊息,並且提高了樣本內泡沫檢定的能力,因為BSADF可以一個一個替除掉樣本進行檢測,若是某個樣本有泡沫發生能夠較為準確的檢定出來,所以 BSADF 在檢定多重泡沫的情況有較大的靈活性。
SADF 是基於每個r_2?[r_0,1]重複進行 ADF 檢定。GSADF 則是對每個r_2?[r_0,1]進行反向的 sup ADF 檢定。根據反向的 sup ADF 序列的 sup 值進行推斷,為
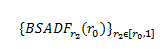
。因此,SADF 與 GSADF 的算式可以分別寫成:
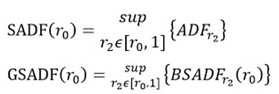
本文內容參考自2015年科技部計畫 - 國際股市價格泡沫預測之研究:理論模型、實證分析應用與比較
若喜歡本文,請關注我們的臉書 Please Like our Facebook Page: Big Data In Finance



留下你的回應
以訪客張貼回應